Conteudos Descritor 2 ( Identificar propriedades comuns e diferenças entre figuras bidimensionais e Tridimensionais, relacionando-as com suas planificações)

Bidimensional/Tridimensional

O que é um mundo bidimensional?

            As duas dimensões são comprimento e largura. Estas em conjunto estabelecem uma superfície plana, sobre a qual podem ser dispostas marcas visíveis planas que não tem profundidade, podem ser figurativas ou abstratas. É uma criação humana. O desenho, a pintura, a impressão, o tingimento ou mesmo a escrita são atividades que levam diretamente a formação do mundo bidimensional.

O mundo Tridimensional

          Vivemos, de fato, em um mundo tridimensional. O que vemos à nossa frente não é uma imagem plana, tendo somente comprimento e largura, mas um espaço com profundidade física, a terceira dimensão.

          Qualquer objeto pequeno, leve e próximo pode ser pego e girado em nossas mãos. Cada movimento do objeto mostra um formato diferente porque a relação o objeto e nossos olhos foi modificada. È na mente humana que o mundo tridimensional ganha o seu significado.

         As dimensões primárias são: comprimento, largura e profundidade. E possuí também: cor, textura, ponto, linha, direção, posição, contrastes...

Trabalha com escultura tridimensional AMILCAR DE CASTRO – 1920-2002 – BRASIL

Planificação de sólidos Geométricos

           A planificação de um sólido geométrico é a apresentação de todas as formas que constituem sua superfície em um plano, ou seja, em duas dimensões. Essas planificações são usadas de várias maneiras, como para calcular a área da superfície de um sólido.
           Confira as planificações dos sólidos geométricos mais conhecidos e um modo de calcular a área do sólido a partir de sua planificação.

Pirâmide

     As pirâmides são sólidos formados por uma base, que pode ser qualquer polígono, e por faces laterais que são obrigatoriamente triângulos. A planificação da pirâmide sempre terá um polígono e alguns triângulos.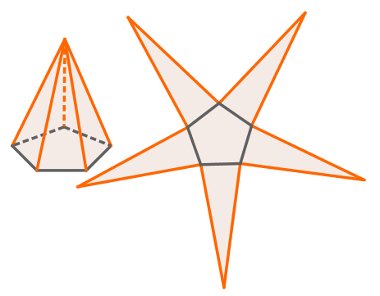

Planificação mais usual de uma pirâmide de base pentagonal

         Perceba que o número de lados da base de uma pirâmide é igual ao número de triângulos que aparecem na sua planificação. Observe também que os triângulos não necessariamente são congruentes (iguais), o que só acontece quando o polígono da base é regular.

Prismas

        Os prismas são sólidos geométricos formados por duas bases, que são polígonos quaisquer congruentes e paralelos, e por faces laterais que sempre são paralelogramos.

          Nos prismas, a quantidade de faces laterais também é igual ao número de lados de uma de suas bases. Sendo assim, sua planificação sempre apresenta dois polígonos congruentes e alguns paralelogramos, que só serão todos iguais se as bases do prisma forem regulares.

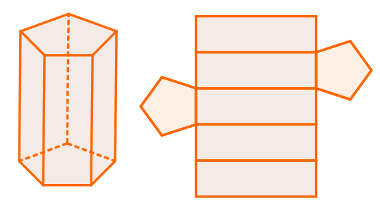
Planificação mais usual de prisma de base pentagonal

Cones

      Os cones são sólidos geométricos formados por um círculo, que é sua base, e por uma superfície curva no formato de funil. As duas figuras geométricas resultantes da planificação de um cone são um setor circular e um círculo. Veja:

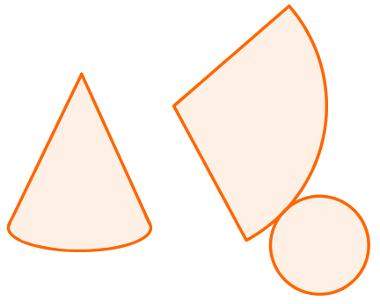
A área dos cones pode ser encontrada pela seguinte expressão:

A = πr(g + r)

Na fórmula, r é o raio do cone e g é a geratriz. 

Exemplo: 

Qual é a área de um cone cuja geratriz mede 10 cm e o raio mede 5 cm?

Solução: substitua esses dados na fórmula acima e considere π = 3,14.

A = πr(g + r)

A = 3,14·5(10 + 5)

A = 15,7·15

A = 235,50 cm²

Cilindros

Os cilindros são sólidos geométricos cujas bases são dois círculos paralelos e congruentes. Em sua planificação, temos dois círculos e um retângulo. Veja:

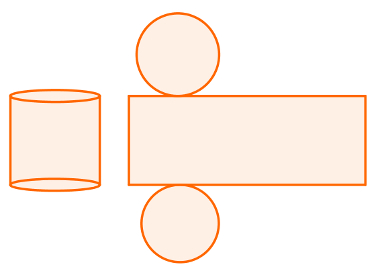
A área do cilindro é determinada pela soma das áreas das duas bases e da superfície lateral. Sabendo que essas figuras são dois círculos congruentes e um retângulo, podemos realizar a seguinte soma:

A = 2A_C + A_R

A = 2πr² + bh

Nessa fórmula, r é o raio do cilindro, h é a sua altura e b é a base do retângulo obtido na planificação. Essa base é exatamente o comprimento do círculo: 2πr.

A = 2πr² + 2πrh

A = 2πr(r + h)

Veja um exemplo de cálculo de área:

Um cilindro possui base circular cujo raio é 2 cm e a altura é 10 cm. Calcule sua área.

Solução: substituindo na fórmula acima os valores dados e considerando π = 3,14, teremos:

A = 2πr(r + h)

A = 2·3,14·2·(2 + 10)

A = 12,56·12

A = 150,72 cm²

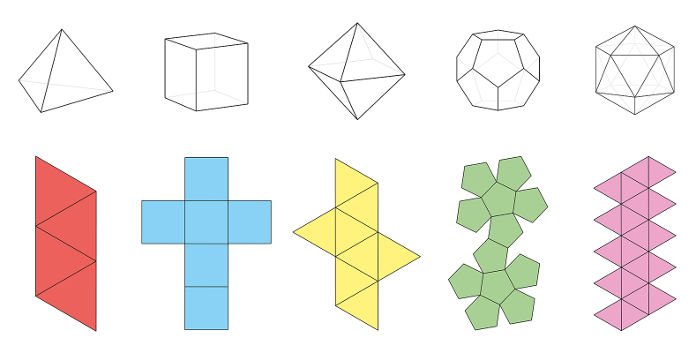
Veja as planificações de alguns sólidos geométricos

bons estudos !